Question

Show that if we have an orthogonal set of vectors φ1, . . . , φk, then φ1, . . . , φk are linearly independent as well, i.e.

Answer 1

Let
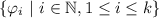
`\\varphi_i~` be a set of orthogonal vectors. By definition of orthogonality, any pairwise dot product between distinct vectors must be zero, i.e.


`\varphi_i\cdot\varphi_j=\begin{cases}\|\varphi_i\|^2&\text{if }i=j\\0&\text{if }i\\eq j\end{cases}`

Suppose there is some linear combination of the
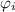
`\varphi_i` such that it's equivalent to the zero vector. In other words, assume they are linearly dependent and that there exist
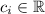
`c_i\in\mathbb R` (not all zero) such that


`\displaystyle\sum_(i=1)^kc_i\varphi_i=c_1\varphi_1+\cdots+c_k\varphi_k=\mathbf 0`

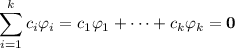
(This is our hypothesis)

Take the dot product of both sides with any vector from the set:


`v_j\cdot\displaystyle\sum_(i=1)^kc_i\varphi_i=c_1\varphi_j\cdot\varphi_1+\cdots+c_k\varphi_j\varphi_k=\varphi_j\cdot\mathbf 0`

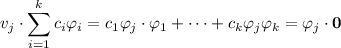
By orthogonality of the vectors, this reduces to


`c_j\|\varphi_j\|^2=0`

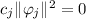
Since none of the
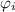
`\varphi_i` are zero vectors (presumably), this means
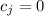
`c_j=0`. This is true for all
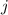
`j`, which means only
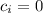
`c_i=0` will allow such a linear combination to be equivalent to the zero vector, which contradicts the hypothesis and hence the set of vectors must be linearly independent.