Question

Hi i dont understand this question, can u do it step by step?

Answer 1

Problem #2

Given the diagram of the statement, we have:

From the diagram, we see that we have two triangles:

Triangle 1 or △ADP, with:

• angle ,θ,,

,

• hypotenuse ,h = AP,,

,

• adjacent cathetus, ac = AD = x cm.

,

• opposite cathetus ,oc = DP,.

Triangle 2 or △OZP, with:

• angle θ,

,

• hypotenuse, h = OP = 4 cm,,

,

• adjacent cathetus, ac = ZP = AP/2,.

(a) △ADP: sides and area

Formula 1) From geometry, we know that for right triangles Pitagoras Theorem states:

`h^2=ac^2+oc^2.`

Where h is the hypotenuse, ac is the adjacent cathetus and oc is the opposite cathetus.

Formula 2) From trigonometry, we have the following trigonometric relation for right triangles:

`\cos \theta=(ac)/(h).`

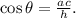
Where:

• θ is the angle,

,

• h is the hypotenuse,

,

• ac is the adjacent cathetus.

(1) Replacing the data of Triangle 1 in Formulas 1 and 2, we have:

`\begin{gathered} AP^2=AD^2+DP^2\Rightarrow DP=\sqrt[]{AP^2-AD^2}=\sqrt[]{AP^2-x^2\cdot cm^2}\text{.} \\ \cos \theta=(AD)/(AP)=(x\cdot cm)/(AP)\text{.} \end{gathered}`

(2) Replacing the data of Triangle 2 in Formula 2, we have:

`\cos \theta=(ZP)/(OP)=(AP/2)/(4cm).`

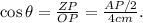
(3) Equalling the right side of the equations with cos θ in (1) and (2), we get:

`(x\cdot cm)/(AP)=(AP/2)/(4cm).`

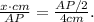
Solving for AP², we get:

`\begin{gathered} x\cdot cm=(AP^2)/(8cm), \\ AP^2=8x\cdot cm^2\text{.} \end{gathered}`

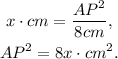
(4) Replacing the expression of AP² in the equation for DP in (1), we have the equation for side DP in terms of x:

`DP^{}=\sqrt[]{8x\cdot cm^2-x^2\cdot cm^2}=\sqrt[]{x\cdot(8-x)}\cdot cm\text{.}`

(ii) The area of a triangle is given by:

`S=(1)/(2)\cdot base\cdot height.`

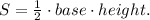
In the case of triangle △ADP, we have:

• base = DP,

,

• height = AD.

Replacing the values of DP and AD in the formula for S, we get:

`S=(1)/(2)\cdot DP\cdot AD=(1)/(2)\cdot(\sqrt[]{x\cdot(8-x)}\cdot cm)\cdot(x\cdot cm)=(x)/(2)\cdot\sqrt[]{x\cdot(8-x)}\cdot cm^2.`

(b) Maximum value of S

We must find the maximum value of S in terms of x. To do that, we compute the first derivative of S(x):

`\begin{gathered} S^(\prime)(x)=(dS)/(dx)=(1)/(2)\cdot\sqrt[]{x\cdot(8-x)}\cdot cm^2+(x)/(2)\cdot(1)/(2)\cdot(8-2x)/(√(x\cdot(8-x)))\cdot cm^2 \\ =(1)/(2)\cdot\sqrt[]{x\cdot(8-x)}\cdot cm^2+(x)/(2)\cdot\frac{(4-x^{})}{\cdot\sqrt[]{x\cdot(8-x)}}\cdot cm^2 \\ =(1)/(2)\cdot\frac{x\cdot(8-x)+x\cdot(4-x)}{\sqrt[]{x\cdot(8-x)}}\cdot cm^2 \\ =\frac{x\cdot(6-x)}{\sqrt[]{x\cdot(8-x)}}\cdot cm^2\text{.} \end{gathered}`

Now, we equal to zero the last equation and solve for x, we get:

`S^(\prime)(x)=\frac{x\cdot(6-x)}{\sqrt[]{x\cdot(8-x)}}\cdot cm^2=0\Rightarrow x=6.`

We have found that the value x = 6 maximizes the area S(x). Replacing x = 6 in S(x), we get the maximum area:

`S(6)=(6)/(2)\cdot\sqrt[]{6\cdot(8-6)}\cdot cm^2=3\cdot\sqrt[]{12}\cdot cm^2=6\cdot\sqrt[]{3}\cdot cm^2.`

(c) Rate of change

We know that the length AD = x cm decreases at a rate of 1/√3 cm/s, so we have:

`(d(AD))/(dt)=(d(x\cdot cm))/(dt)=(dx)/(dt)\cdot cm=-\frac{1}{\sqrt[]{3}}\cdot(cm)/(s)\Rightarrow(dx)/(dt)=-\frac{1}{\sqrt[]{3}}\cdot(1)/(s)\text{.}`

The rate of change of the area S(x) is given by:

`(dS)/(dt)=(dS)/(dx)\cdot(dx)/(dt)\text{.}`

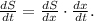
Where we have applied the chain rule for differentiation.

Replacing the expression obtained in (b) for dS/dx and the result obtained for dx/dt, we get:

`(dS)/(dt)(x)=(\frac{x\cdot(6-x)}{\sqrt[]{x\cdot(8-x)}}\cdot cm^2\text{)}\cdot(-\frac{1}{\sqrt[]{3}}\cdot(1)/(s)\text{)}`

Finally, we evaluate the last expression for x = 2, we get:

`(dS)/(dt)(2)=(\frac{2\cdot(6-2)}{\sqrt[]{2\cdot(8-2)}}\cdot cm^2\text{)}\cdot(-\frac{1}{\sqrt[]{3}}\cdot(1)/(s))=-\frac{8}{\sqrt[]{12}}\cdot\frac{1}{\sqrt[]{3}}\cdot(cm^2)/(s)=-\frac{8}{\sqrt[]{36}}\cdot(cm^2)/(s)=-(8)/(6)\cdot(cm^2)/(s)=-(4)/(3)\cdot(cm^2)/(s).`

So the rate of change of the area of △ADP is -4/3 cm²/s.

Answers

(a)

• (i), Side DP in terms of x:

`DP(x)=\sqrt[]{x\cdot(8-x)}\cdot cm\text{.}`

• (ii), Area of ADP in terms of x:

`S(x)=(x)/(2)\cdot\sqrt[]{x\cdot(8-x)}\cdot cm^2.`

(b) The maximum value of S is 6√3 cm².

(c) The rate of change of the area of △ADP is -4/3 cm²/s when x = 2.