Question

A pottery wheel with rotational inertia 40 kgm^2 rotates at 10 rev/s. 4 kg of clay is dropped onto the wheel 1.2 m from the axis. What angular speed will the wheel have after this?1. 55 rad/s2. 8.7 rad/s3. 70 rad/s4. 0 rad/s

Answer 1

Given:

• Rotational inertia = 40 kg.m²

,

• Initial angula speed = 10 rev/s

,

• Mass, m = 4 kg

,

• Diameter, d = 1.2 m

Let's find the angular speed of the wheel.

To find the angular speed, apply the formula:

`L_i=(I+md^2)*w_f`

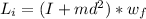
Where wf is the final angular speed

I is the rotational inertia

m is the mass

d = 1.2

Li is the angular momentum.

To find the angular momentum, we have:

`\begin{gathered} L_i=40*10*2\pi \\ L_i=2513.27\text{ kg.m}^2\text{ rad/s} \end{gathered}`

Now, to find the final angular speed, wf, plug in values in the first equation and solve for wf:

`\begin{gathered} Li=(I+md^2)w_f \\ \\ 2513.27=(40+4*1.2^2)w_f \\ \\ 2513.27=45.76w_f \\ \\ w_f=(2513.27)/(45.76) \\ \\ w_f=54.9\approx55\text{ rad/s} \end{gathered}`

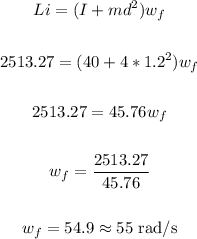
Therefore, the final angular speed is 55 rad/s.

ANSWER:

1.) 55 rad/s