To find the resultant force we will first find the component force of the forces given, to do this, we need to remember that any vector can be express in component form by:
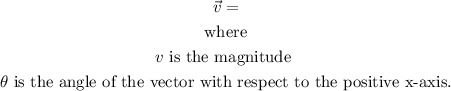
For force u we notice that its magnitude is 280 N and its angle is zero, then we have:
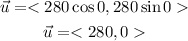
For force v we know that its magnitude is 135 N and its angle is 45°, then we have:
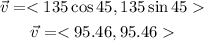
Now that we have both vectors in component form we add them to get the resultant in component form:
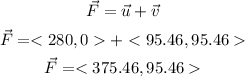
Once we have the resultant force in component form we can find its magnitude and direction if we remember that they are given by:
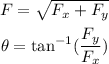
Plugging the values we found for the components we have:
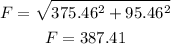
and
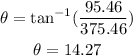
Therefore, the magnitude of the resultant force is 387.41 N and the direction is 14.27°