Question

Select the table of values that contains ordered pairs that, when plotted, provide the best representation of the curve of the function

Answer 1

As given by the question

There are given that the equation:

`y=-2(x+3)^2+4`

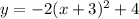
Now,

Put the value of x into the given equation and find the value of y from all the tables one-by-one and match their value of x and y are equal or not.

Then,

Form the option third,

Put x = -2 to find the value of y, then match the value of y with the given value of y in the table.

So,

`\begin{gathered} y=-2(x+3)^2+4 \\ y=-2(-2+3)^2+4 \\ y=-2(1)^2+4 \\ y=-2+4 \\ y=2 \end{gathered}`

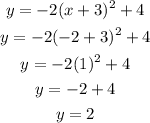
Now,

Put x = -1, then:

`\begin{gathered} y=-2(x+3)^2+4 \\ y=-2(-1+3)^2+4 \\ y=-2(2)^2+4 \\ y=-2(4)+4 \\ y=-8+4 \\ y=-4 \end{gathered}`

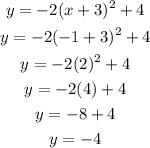
Then,

Put x = 0, then:

`\begin{gathered} y=-2(x+3)^2+4 \\ y=-2(0+3)^2+4 \\ y=-2(3)^2+4 \\ y=-2(9)+4 \\ y=-18+4 \\ y=-14 \end{gathered}`

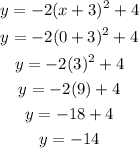
Then,

Put 1 into the given equation instead of x:

So,

`\begin{gathered} y=-2(x+3)^2+4 \\ y=-2(1+3)^2+4 \\ y=-2(4)^2+4 \\ y=-2(16)+4 \\ y=-32+4 \\ y=-28 \end{gathered}`

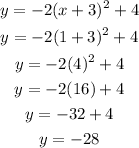
And,

Put x = 2, so:

`\begin{gathered} y=-2(2+3)^2+4 \\ y=-2(5)^2+4 \\ y=-2(25)+4 \\ y=-50+4 \\ y=-46 \end{gathered}`

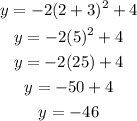
Now,

From option d, all values of x and y are matched also but curve representation is matched in option D.

Hence, the correct option is D.