Question

A tree on a hillside casts a shadow c = 215 ft down the hill. If the angle of inclination of the hillside is b = 23° to the horizontal and the angle of elevation of the sun is a = 53, find the height of the tree. (Round your answer to the nearest foot.)

Answer 1

This is the figure, roughly. We want h.

Using smaller triangle, we can write:

`\begin{gathered} \text{Cos}23=(x)/(215) \\ x=215\cdot\cos 23 \\ x=197.9 \end{gathered}`

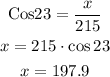
Also,

`\begin{gathered} y=215\cdot\sin 23 \\ y=84 \end{gathered}`

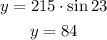
Now, taking the larger triangle:

The angle is 53 (30 + 23).

Let the larger side (right side) be m, which is basically:

m = h + y

Let's find m:

`\begin{gathered} \tan 53=(m)/(x) \\ \tan 53=(m)/(197.9) \\ m=197.9\cdot\tan 53 \\ m=262.62 \end{gathered}`

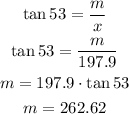
Now, we want height, h, which is:

m = h + y

262.62 = h + 84

h = 262.62 - 84

h = 178.62

Rounded to nearest feet

h = 179 feet