Question

Tom simplified an expression in three steps, as shown:

x to the power of negative 2 multiplied by y to the power of 4, over y multiplied by x to the power of 4 multiplied by x to the power of 4 multiplied by y to the power of negative 2, the whole to the power of 4 equal to x to the power of 2 multiplied by y to the power of 8, over y to the power of 4 multiplied by x to the power of 8 multiplied by x to the power of 8 multiplied by y to the power of 2 equal to x to the power of 2 multiplied by y to the power of 8, over y to the power of 6 multiplied by x to the power of 16.

Which is the first incorrect step and why?

Step 1, all the exponents are increased by 4
Step 2, the exponents of the same base are added during multiplication
Step 3, the exponents of the same base are subtracted during division
Step 3, all the exponents are added during division

Answer 1

The answer would be (A) Step 1, all the exponents are increased by 4

Explanation:

Answer 2

1.
`[(x^(-2)* y^4)/(y)} }* x^4* x^ 4 * y^(-2)]^(4)=2.(x^2 * y^8)/(y^4) }* x^8 * x^8* y^2=3. (x^2* y^8)/(y^6)* x^(16)`

As we have to solve the radicals inside the bracket, first by adding and subtracting exponents of same bases, then we have to multiply the exponent by 4.

→Use this property of radicals to solve the radicals inside the bracket:

`(a^m)/(a^n)=a^(m-n) \\\\ a^m * a^n=a^(m+n) \\\\(a^(m))^(n)=a^(mn)`

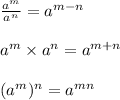
Step 1, all the exponents are increased by 4 is the first incorrect step among all four steps described in the question.