Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.

What is the length of B'B?

Answer 1

its -2 and nothing else can be it

Answer 2

5.39 units.

Explanation:

We have been given an image of two squares on coordinate plane. We are asked to find the length of B'B.

We will use distance formula to solve our given problem.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

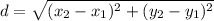
Let point
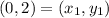`(0,2)=(x_1,y_1)` and
`(5,4)=(x_2,y_2)`.

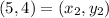Upon substituting coordinates of our given points in distance formula, we will get:

`d=√((5-0)^2+(4-2)^2)`

`d=√((5)^2+(2)^2)`

`d=√(25+4)`

`d=√(29)`

`d=5.3851\approx 5.39`

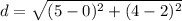
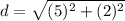
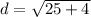
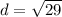
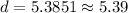
Therefore, the length of B'B is approximately 5.39 units.