Question

The scatter plot below shows the number of pizzas sold during weeks when different numbers of coupons were issued. The equation represents the linear model for this data.

y = 3.4x + 43



According to the model, what is the average number of pizzas sold in one night if no coupons are issued?



A. 0

B. 21

C. 43

D. 60

E. 70

Answer 1

The correct answer option C.

Explanation:

Let x be the number of coupons issued.

Let y be the number of the pizzas sold.

The given equation:

`y=3.4x+43`

This given equation of an straight line.

Number of pizzas when no coupons were issued.

`y=3.4x+43=3.4* 0+43=43`

43 number of pizzas were sold in one night.

Hence, the correct answer option C.

Answer 2

The average number of pizzas sold in one night if no coupons are issued is 43.

Explanation:

In the scatter plot the average number of pizzas sold is represented on x and number of coupons issued is represented on y.

The trend line of this linear model is
`y = 3.4x + 43`

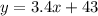
So, when no coupons are issued then the value of x becomes 0, then putting the value of x in the equation,

`\Rightarrow y=3.4(0)+43`

`\Rightarrow y=0+43`

`\Rightarrow y=43`

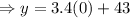
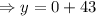
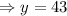
Therefore, the average number of pizzas sold in one night if no coupons are issued is 43.