so... our numbers... let's say the first one is hmmm "a"
so the second and subsequent are
a
a+1
a+2
a+3
a+4
there, 5 consecutive whole numbers or integers for that matter
now, we know the sum of the square of the first three,
is the same as the sum of the square of the last two
so
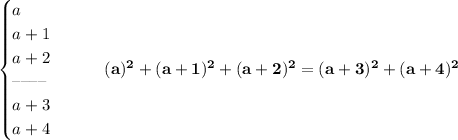
do a binomial theorem expansion on those, solve for "a"