notice the picture below
the AD line is a bisector, cutting the 36 degrees A in half,
18 and 18 degrees each half
notice the tickmarks, the triangle is an isosceles,
if those two sides are equal, so are the angles they make
down below with the base
now, the base is 8, AD is bisecting that too, to 4 and 4
now, using the Law of Sines
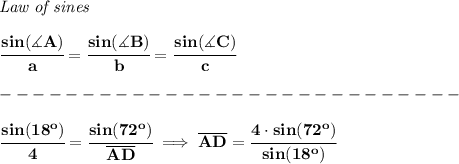
keep in mind, the angles are in degrees, so, when taking the sines, make sure your calculator is in Degree mode