Answer:
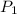 = 2
= 2
 = k(k+1)
= k(k+1)
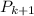 = (k+1)(k+2)
= (k+1)(k+2)
Explanation:
We are given the statement,
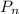 as 2 + 4 + 6 + . . . + 2n = n(n+1)
as 2 + 4 + 6 + . . . + 2n = n(n+1)
That is,
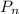 as 2 + 4 + 6 + . . . + 2n =
as 2 + 4 + 6 + . . . + 2n =
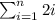
So, we have,
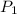 =
=
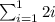 = 2
= 2
 =
=
 = 2 + 4 + 6 + . . . + 2k = k(k+1)
= 2 + 4 + 6 + . . . + 2k = k(k+1)
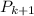 =
=
 = 2 + 4 + 6 + . . . + 2k + 2(k+1) = (k+1)(k+2)
= 2 + 4 + 6 + . . . + 2k + 2(k+1) = (k+1)(k+2)
Thus, we get,
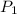 = 2
= 2
 = k(k+1)
= k(k+1)
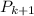 = (k+1)(k+2)
= (k+1)(k+2)