Question

The Gravitron is a ride that rotates around a central axis until it reaches a certain velocity and the riders are pinned to the walls. Once this occurs, the floor is lowered until the riders are suspended above the floor. The Gravitron has a radius of 3.00 meters and reaches a speed of 15.0 m/s. Dalnita has a mass of 55.0 kg. What is her angular velocity in radians per second?

Answer 1

Sounds like you've been given some unnecessary information.
The linear velocity "v" and angular velocity "w" of something in circular motion of radius "R" are related as;

v = Rw

You are given v= 15 m/s and R = 3 m , so just solve for "w".

Answer 2

Angular velocity of Dalnita,
`\omega=5\ rad/s`

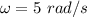
Step-by-step explanation:

It is given that,

The radius of Gravitron, r = 3 m

Speed of gravitron, v = 15 m/s

Dalnita's mass, m = 55 kg

We need to find her angular velocity. The relationship between the angular velocity and linear speed is as follows :

`v=r* \omega`

`\omega=(v)/(r)`

`\omega=(15\ m/s)/(3\ m)`

`\omega=5\ rad/s`

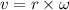
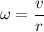
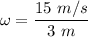
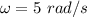
So, her angular speed is 5 radian per second. Hence, this is the required solution.