Since this is an arithmetic progression, the sequence is defined recursively by
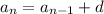
where
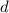
is the common difference and
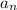
is the

th term. Solving for
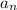
gives
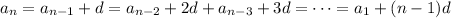
Adding up the first 16 terms gives
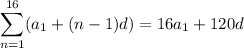
Adding up the next 16 terms gives
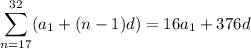
So you have two equations with two unknowns,
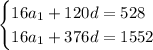
Solving gives
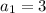
and
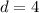
.