Question

Use Gauss-Jordan elimination to solve the following linear system.

–x + 6y = 20
–x + 3y = 8

A. (–2,–2)
B. (3,2)
C. (4,4)
D. (0,5)

Answer 1

the answer would be C. (4,4)

Answer 2

The correct option is C) (4,4)

Explanation:

Given linear system is :

`-x+6y=20`

`-x+3y=8`

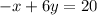
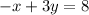
Solve using Gauss - jordan elimination

It is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix.

`\:\begin{pmatrix}-1&6&20\\ \:-1&3&8\end{pmatrix}`

`\mathrm{Reduce\:matrix\:to\:row\:echelon\:form}\:\begin{pmatrix}a&\cdots &b\\ 0&\ddots &\vdots \\ 0&0&c\end{pmatrix}`

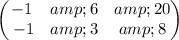
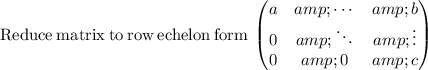
Divide row(1) by -1

`\begin{pmatrix}1&-6&-20\\ \:-1&3&8\end{pmatrix}`

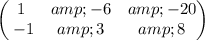
Add row(1) to row(2)

`\begin{pmatrix}1&-6&-20\\ \:0&-3&-12\end{pmatrix}`

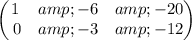
Divide row(2) by -3

`\begin{pmatrix}1&-6&-20\\ \:0&1&4\end{pmatrix}`

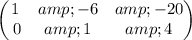
Add (6 * row(2) ) to row(1)

`=\begin{pmatrix}1&0&4\\ 0&1&4\end{pmatrix}`

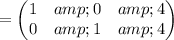
Hence the corresponding values of x and y are (4, 4)

Therefore, the correct option is C) (4,4)