Question

What is the slope of a line perpendicular to the line whose equation is15x + 12y = -108. Fully reduce your answer.Answer:Submit Answer

Answer 1

GIven:

The equation of a line is 15x+12y=-108.

The objective is to find the slope of the perpencidular line.

It is known that the equation of straight line is,

`y=mx+c`

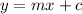
Here, m represents the slope of the equation and c represents the y intercept of the equation.

Let's find the slope of the given equation by rearranging the eqation.

`\begin{gathered} 15x+12y=-108 \\ 12y=-108-15x \\ y=-(15x)/(12)-(108)/(12) \\ y=-(5)/(4)x-9 \end{gathered}`

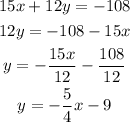
By comparing the obtained equation with equation of striaght line, the value of slope is,

`m_1=-(5)/(4)`

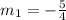
THe relationship between slopes of a perpendicular lines is,

`\begin{gathered} m_1\cdot m_2=-1 \\ -(5)/(4)\cdot m_2=-1 \\ m_2=-1\cdot(-(4)/(5)) \\ m_2=(4)/(5)^{} \end{gathered}`

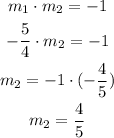
Hence, the value of slope of perpendicular line to the given line is 4/5.