Question

Find a closed form expression for the nth right Riemann sum of this integral?

Answer 1

Partitioning the interval
`[6,11]` into
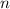
`n` equally-spaced subintervals gives
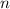
`n` rectangles of width
`\Delta x=\frac{11-6}n=\frac5n` and of heights determined by the right endpoints of each subinterval.

If
`a=x_1=6`, then
`x_2=6+\frac5n`,
`x_3=6+2\frac5n`, and so on, up to
`b=x_(n+1)=6+n\frac5n=11`. Because we're using the right endpoints, the approximation will consider
`x_2,\ldots,x_(n+1)`

The definite integral is then approximated by


`\displaystyle\int_6^(11)(1-5x)\,\mathrm dx\approx\sum_(i=2)^(n+1)f(x_i)\Delta x=\sum_(i=2)^(n+1)\left(1-\left(6+(i-1)\frac5n\right)\frac5n`

You have


`\displaystyle\sum_(i=2)^(n+1)\left(1-5\left(6+(i-1)\frac5n\right)\frac5n=\sum_(i=2)^(n+1)\left(-29-\frac{25}n(i-1)\right)\frac5n`

`=\displaystyle-{145}n\sum_(i=2)^(n+1)1-(125)/(n^2)\sum_(i=2)^(n+1)(i-1)`

`=-145-(125(n^2+n))/(2n^2)`

`=-\frac{145}2-(125)/(2n)`

To check that this is correct, let's make sure the sum converges to the exact value of the definite integral. As
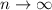
`n\to\infty`, you have the sum converging to
`-\frac{145}2`.

Meanwhile,


`\int_6^(11)(1-5x)\,\mathrm dx=\left[x-\frac52x^2\right]_(x=6)^(x=11)=-\frac{415}2`

so we're done.