Question

Find the local maximum and minimum values and saddle point(s) of the function.

Answer 1

`f(x,y)=9e^y(y^2-x^2)`

`\\abla f=\left\langle-18xe^y,9ye^y(2+y)\right\rangle`

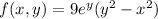
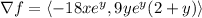
Critical points occur where the gradient is zero. This is guaranteed whenever
`x=0` and either
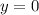
`y=0` or
`y=-2`.

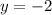
The Hessian matrix for this function looks like


`H(x,y)=\begin{bmatrix}f_(xx)&f_(xy)\\f_(yx)&f_(yy)\end{bmatrix}=\begin{bmatrix}-18e^y&-18xe^y\\-18xe^y&9e^y(2-x^2+4y+y^2)\end{bmatrix}`

and has determinant


`|H(x,y)|=-162e^(2y)(2+x^2+4y+y^2)`

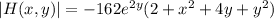
Maxima occur whenever the determinant is positive and
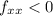
`f_(xx)<0`. Minima occur whenever both the determinant and
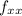
`f_(xx)` are positive. Saddle points occur whenever the determinant is negative.

At
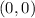
`(0,0)`, you have a saddle point since the determinant reduces to -324, so
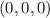
`(0,0,0)` is the saddle point.

At
`(0,-2)`, the determinant is
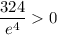
`(324)/(e^4)>0` and
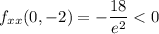
`f_(xx)(0,-2)=-(18)/(e^2)<0`, so
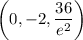
`\left(0,-2,(36)/(e^2)\right)` is a local maximum.

No other critical points remain, so you're done.