Question

Q1 How many subsets of a set with 100 elements have morethan one element ?

Q2 How many strings of four decimal digits

a) do not cantain the same digit twice?

b) end with even digit ?

c) have exactly three digits that are 9s ?

Answer 1

A set of
`n` elements has
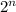
`2^n` possible subsets, where two classes of those sets are the empty set (1) and all the possible singleton sets (
`n`). So a set of
`n` elements has
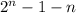
`2^n-1-n` possible subsets with more than one elements. For Q1 take
`n=100`.

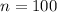
Q2a. Assuming not containing the same digits twice also includes not numbers with three or four of the same digit, and assuming digits are chosen from the usual 0-9, there are


`4!\dbinom{10}4=(4!10!)/(4!(10-4)!)=10*9*8*7=5040`

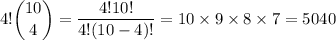
possible strings.

Q2b. The first three digits can be chosen freely from 0-9, while the last digit has to be one of 0, 2, 4, 6, or 8. This means you have


`10^3*5=5000`

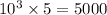
possible strings

Q2c. Any such string will take the form
`999X`,
`99X9`,
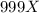
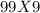
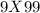
`9X99`, or
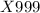
`X999`, where
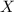
`X` has 9 possible choices (0-9 excluding 9, since we want exactly three 9s in any such string). So there are


`4*9=36`

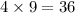
possible strings.