Question

Jan 10, 7:17:08 PM Which equation represents a line which is perpendicular to the line x - 2y = -14? Oy= -27 -1 Oy= 2x + 8 Submit Answer Oy=x+4 Oy = -x + 2

Answer 1

You need to determine which line is perpendicular to the line

`x-2y=-14`

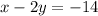
For two lines to be considered perpendicular their slopes must be the inverse positive, that is, if, for example, you have the lines

`y_1=mx_1+b`
`y_2=nx_2+c`

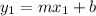
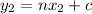
For them to be perpendicular one slope must be the inverse negative of the other such as

`n=-(1)/(m)`

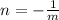
The first step is to write the given line in slope-intercept form:

1) Pass the x term to the right side of the equal sign

`\begin{gathered} x-2y=-14 \\ x-x-2y=-14-x \\ -2y=-x-14 \end{gathered}`

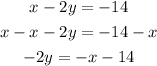
2) Divide both sides of the expression by "-2"

`\begin{gathered} -(2y)/(-2)=-(x)/(-2)-(14)/(-2) \\ y=(1)/(2)x+7 \end{gathered}`

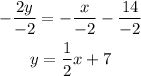
The slope of the line is

`m=(1)/(2)`

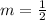
So the slope of a line perpendicular to it will be the inverse negative of it

`\begin{gathered} n=-((1)/((1)/(2))) \\ n=-2 \\ \end{gathered}`

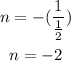
The correct option is the one that has slope -2