Question

PLEASE SOLVE AND SHOW WORK Find the equation of the line that passes through the points (-1,-5) and (-7,-6) in slope intercept form

Answer 1

The way that you find this problem is to first find the slope, and then input one of your points into your equation to find b.
The slope-intercept form of a line is:
`y=mx+b`, where m is the slope and b is the y-intercept.

To find the slope, you must use the following equation:

`(y_(2)-y_(1))/(x_(2)-x_(1))`

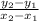
In this equation, this would be equivalent to:
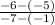
`(-6-(-5))/(-7-(-1))` which, when simplified, is
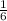
`(1)/(6)`. This is your slope.

To find the Y-intercept, you just plug all variables that you currently have solved for into the equation. You may use either point for the x and y variables, but you must use
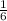
`(1)/(6)` for the m term.


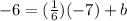
`-6 = ((1)/(6))(-7) + b` leads to
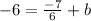
`-6 = (-7)/(6) +b` which leads to
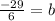
`(-29)/(6) = b`. You have now solved for the y-intercept and aare ready to form your final equation.

The final equation is:
`y=(1)/(6)x -(29)/(6)`