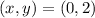Question

I will show you the pic

Answer 1

We are given the following system of equations:

`\begin{gathered} 6x-4y=-8,(1) \\ y=-6x+2,(2) \end{gathered}`

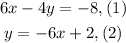
To solve this system by substitution we will replace the value of "y" from equation (2) in equation (1)

`6x-4(-6x+2)=-8`

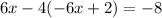
Now we use the distributive property:

`6x+24x-8=-8`

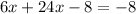
Now we add like terms:

`30x-8=-8`

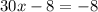
Now we add 8 to both sides:

`30x-8+8=-8+8`

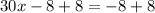
Solving the operations:

`30x=0`

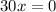
Dividing by 30:

`x=(0)/(30)=0`

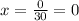
Therefore x = 0. Now we replace the value of "x" in equation (2):

`\begin{gathered} y=-6x+2 \\ y=-6(0)+2 \\ y=2 \end{gathered}`

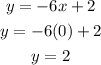
Therefore, the solution of the system is:

`(x,y)=(0,2)`