Question

Let f(x)=1/x and g(x)=x^2+5x find (f×g)(x)

Answer 1

just multiply
remember the distributive proeprty a(b+c)=ab+ac
(f *g)(x)=f(x)g(x)=(1/x)(x^2+5x)=(x^2/x)+(5x/x)=x+5

(f*g)(x)=x+5

Answer 2

(f×g)(x) = x +5.

Explanation:

Given : f(x)=
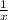`(1)/(x)` and g(x) = x²+5x.

To find : find (f×g)(x).

Solution: We have given f(x)=
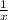`(1)/(x)` and g(x) = x²+5x.

For (f×g)(x) = f(x) * g(x) .

Plug the values

(f×g)(x) =
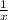`(1)/(x)` * x²+5x.

(f×g)(x) =
`(x^(2)+5x )/(x)`

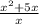
On taking x common from the numerator

(f×g)(x) =
`(x(x+5))/(x)`.

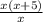(f×g)(x) = x +5.

Therefore, (f×g)(x) = x +5.