Question

The length is twice the sum of its width 3. What are the dimension of the rectangle if it’s area 216 square inches?

Answer 1

Assume that the width of the rectangle = x

Since the length is twice the sum of the width and 3, then

`\begin{gathered} L=2(x+3) \\ L=2x+6 \end{gathered}`

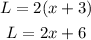
Since the area of the rectangle is 216 square inches, then

Multiply the length and the width, then equate the product by 216

`\begin{gathered} (x)(2x+6)=216 \\ 2x^2+6x=216 \end{gathered}`

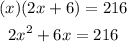
Divide all terms by 2 to simplify

`\begin{gathered} (2x^2)/(2)+(6x)/(2)=(216)/(2) \\ x^2+3x=108 \end{gathered}`

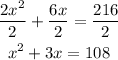
Subtract 108 from both sides

`\begin{gathered} x^2+3x-108=108-108 \\ x^2+3x-108=0 \end{gathered}`

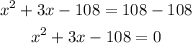
Now, let us factorize the trinomial into 2 factors

`\begin{gathered} x^2=(x)(x) \\ -108=(-9)(12) \\ (x)(-9)+(x)(12)=-9x+12x=3x \end{gathered}`

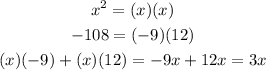
Then the factors are

`x^2+3x-108=^{}(x-9)(x+12)`

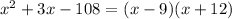
Equate them by 0

`(x-9)(x+12)=0`

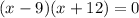
Equate each factor by 0, then find the values of x

`x-9=0`

Add 9 to both sides

`\begin{gathered} x-9+9=0+9 \\ x=9 \end{gathered}`
`x+12=0`

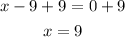
Subtract 12 from both sides

`\begin{gathered} x+12-12=0-12 \\ x=-12 \end{gathered}`

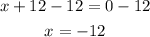
Since the width can not be a negative number (no negative length)

Then the width of the rectangle = 9

Let us find the length

`\begin{gathered} L=2(9)+6 \\ L=18+6 \\ L=24 \end{gathered}`

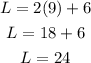
Then the dimensions of the rectangle are 9 inches and 24 inches