Question

A company has a total of 6,500 computers, and 1 week ago, one of those computers was infected with a virus. In each of the next 7 days, the number of computers newly infected with the virus that day has been 3 times what it was the previous day. If the computer virus has not yet been removed from any of the computers that have been infected, how many of the office's computers are not infected with the virus?

A) 1,093 B) 3,220 C) 3,280 D) 5,407

Answer 1

D) 5,407 The Office's Computers Are Not Infected With The Virus.

Answer 2

5407

Explanation:

We are given that A company has a total of 6,500 computers, and 1 week ago, one of those computers was infected with a virus.

In each of the next 7 days, the number of computers newly infected with the virus that day has been 3 times what it was the previous day.

Initially no. of computers infected with virus = 1

Since we are given that every day the no. of infected computers will be 3 times the no. of infected computers on previous day

So, no. of infected computers on 2nd day = 3

No. of infected computers on 3rd day = 383 = 9

So, the sequence becomes: 1,3,9 ,.....

Since G.P. is formed

So, common ratio r =
`(3)/(1) =(9)/(3)=3`

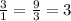
Sum of n terms in G.P. =
`S_n=(a(1-r^n))/(1-r)`

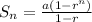
Where a is the initial term

n = no. of terms

r = common ratio

Now no. of infected computers after 7 days will be :

`S_7=(1(1-3^n))/(1-3)`

`S_7=1093`

Thus the no. of infected computers are 1093

So, no. of infected computers = Total computers - infected computers

=6500-1093

=5407

Hence the no.of office's computers are not infected with the virus is 5407