Question

A hiker leaves her camp and walks 3.5 km in a direction of 55° south of west to the lake. after a short rest at the lake, she hikes 2.7 km in a direction of 16° east of south to the scenic overlook. what is the magnitude of the hiker’s resultant displacement? round your answer to the nearest tenth

Answer 1

1.3km

Step-by-step explanation:

We need to get the total displacement of the x and y components.

taking north and east as positive:

`d_(1x)=-3.5km*cos(55^o)=-2km\\d_(2x)=2.7km*sin(16^o)=0.74km\\d_x=0.74km-2km=-1.26km`

`d_(1y)=-3.5km*sin(55^o)=-2.9km\\d_(2y)=-2.7km*sin(16^o)=-2.6km\\d_y=-2.6km-2.9km=-5.5km`

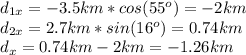
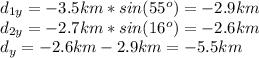
The magnitude of the displacement is given by:

`d=√((d_x)^2+(d_y)^2)\\d=√((-1.26)^2+(-0.3)^2)=5.64km`

We were told to round it to the nearest tenth, so we have to look at the hundredth place, because it is equal or less than 4, the tenth place remains the same and we drop the numbers to the right.

d=5.6km

Answer 2

Let's choose east as positive x-direction and south as positive y-direction. We can resolve the two displacement along these two axes:

- Displacement 1 (3.5 km,
`55^(\circ)` south of west

`d_(1x)=-(3.5 km)( cos 55^(\circ))=-2.01 km`

`d_(1y)=(3.5 km)( sin 55^(\circ))=2.87 km`

- Displacement 2 (2.7 km,
`16^(\circ)` east of south

`d_(2x)=(2.7 km)( sin 16^(\circ))=0.74 km`

`d_(1y)=(2.7 km)( cos 16^(\circ))=2.60 km`

So, the total components on the two directions are

`d_x = -2.01 km+0.74 km=-1.27 km`

`d_y=2.87 km+2.60 km=5.47 km`

And the magnitude of the hiker's resultant displacement is

`d=√((1.27 km)^2+(5.47 km)^2)=5.6 km`