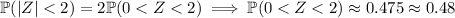Question

The sat mathematics score in the state of florida for this year are approximately normally distributed with a mean of 500 and standerd deviation of 100.

Answer 1

Since
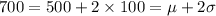
`700=500+2*100=\mu+2\sigma` is 2 standard deviations above the mean, you're looking for the probability that


`\mathbb P(0<Z<2)`

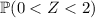
The empirical rule says that approximately 95% of a normal distribution lies within 2 standard deviations of the mean, or
`\mathbb P(|Z|<2)\approx0.98`.

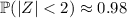
Since the normal distribution is symmetric, you have


`\mathbb P(|Z|<2)=2\mathbb P(0<Z<2)\implies \mathbb P(0<Z<2)\approx0.475\approx0.48`