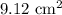Solution:
Given the figure below:
The area of the shaded region is expressed as
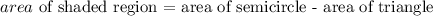
step 1: Evaluate the area of the semicircle.
The area of the semicircle is expressed as

Thus, we have
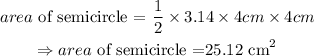
step 2: Evaluate the area of the triangle.
The area of the triangle is expressed as
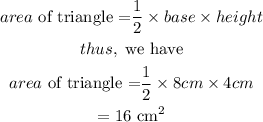
step 3: Evaluate the area of the shaded region.
Recall that
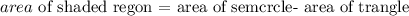
Thus, we have
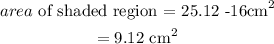
Hence, the area of the shaded region is