Question

Ready for me for a quadratic function with vertex (3,9)

Answer 1

We have to write an equation of a quadratic function that has a vertex at (3,9) and pass through the origin.

We can use the vertex form of the quadratic equation:

`y=a(x-h)^2+k`

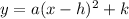
where the vertex has coordinates (h,k).

In this case, (h,k) = (3,9).

From the formula we can see that the parameter a that can take any value and still have the same vertex. We will use the parameter "a" to make it pass through the origin.

The vertex form of the equation is then:

`y=a(x-3)^2+9`

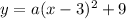
As it pass through the origin, then the equation should be satisfied when x = 0 and y = 0:

`\begin{gathered} 0=a(0-3)^2+9 \\ 0=a(-3)^2+9 \\ 0=a\cdot9+9 \\ -9=9a \\ -(9)/(9)=a \\ a=-1 \end{gathered}`

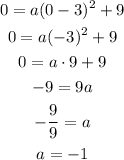
Then, as a = -1, we can write the equation as:

`y=-(x-3)^2+9`

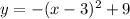
Answer: An example of quadratic function with vertex (3,9) that pass through the origin is y = -(x-3)² + 9.