Question

Empirical evidence suggests that 25% of Florida drivers are uninsured.

If four random Florida drivers are involved in an accident, what is the probability that more than one of them are uninsured?

Answer 1

If the question is asking if only one isnt insured, the chances are 1/12.
If the question is asking if at least one isnt insured, the chances are 1/4.

Answer 2

The probability is 0.2617

Explanation:

The variable that said the number of drivers that are uninsured follow a binomial distribution, so the probability that x drivers are uninsured is calculated as:

`P(x)=(n!)/(x!(n-x)!)*p^(x)*(1-p)^(n-x)`

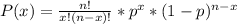
Where n is the number of drivers involved in an accident and p is the probability that any driver is uninsured, then:

`P(x)=(4!)/(x!(4-x)!)*0.25^(x)*(1-0.25)^(4-x)`

So, the probability that more than one of them are uninsured is:

P(x>1) = P(2) + P(3) + P(4)

Therefore, the values of P(2), P(3) and P(4) are:

`P(2)=(4!)/(2!(4-2)!)*0.25^(2)*(1-0.25)^(4-2)=0.2109`

`P(3)=(4!)/(3!(4-3)!)*0.25^(3)*(1-0.25)^(4-3)=0.0469`

`P(x)=(4!)/(4!(4-4)!)*0.25^(4)*(1-0.25)^(4-4)=0.0039`

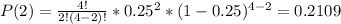
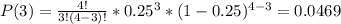
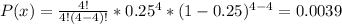
Finally, the probability that more than one of them are uninsured is:

P(x>1) = 0.2109 + 0.0469 + 0.0039 = 0.2617