Question

What is the length of AC

Answer 1

first you set up a proportion: 51/144-x=3/x
cross multiply: 51x=432-3x
add 3x to each side: 54x=432
divide each side by 54: x=8
now put x into 144-x: 144-(8)
simplify: 136
The correct answer is A.136

Answer 2

Option A is correct.

The length of AC = 136 unit.

Step-by-step explanation:

AA(Angle-Angle) similarity postulate states that two triangles are similar if they have two corresponding angles that are congruent or equal in measure.

First show that ΔBAC and ΔDEC are similar triangle.

In ΔBAC and ΔDEC

`\angle BAC = \angle DEC = 90^(\circ)` [Angle] [Given in figure]

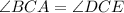`\angle BCA =\angle DCE` [Angle] [Given]

then, by AA postulates we can say that ;

`\triangle BAC \sim \triangle DEC`

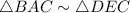
In similar triangle, their corresponding sides are in proportion.

Therefore, in ΔBAC and ΔDEC

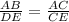`(AB)/(DE)= (AC)/(CE)` ......[1]

from the figure, we have

AB = 51 unit , AC = 144-x unit , DE =3 unit and CE =x unit.

Substitute these in [1] to solve for x;

`(51)/(3)= (144-x)/(x)`

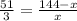
Simplify:

`17= (144-x)/(x)`

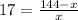
By cross multiply we get;

`17x =144-x`

or

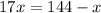
`17x+x =144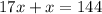` or

18x =144

Divide both sides by 18 we get;

x = 8.

Then, the length of AC = 144-x =144-8 = 136 unit.