Question

HELP{

Which conclusion about f(x) and g(x) can be drawn from the table?

The functions f(x) and g(x) are reflections over the x-axis.

The functions f(x) and g(x) are reflections over the y-axis.

The function f(x) is a decreasing function, and g(x) is an increasing function.

The function f(x) has a greater initial value than g(x).

Answer 1

The correct answer is B) The functions f(x) and g(x) are reflections over the y-axis.

Explanation:

Hope this helps! :)

Answer 2

Answer: The correct conclusion is(B) The functions f(x) and g(x) are reflections over the y-axis.

Step-by-step explanation: Two functions f(x) and g(x) are given as follows:

`f(x)=2^x,~~~~~~~g(x)=\left((1)/(2)\right)^x.`

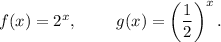
We know that if f(-x) = g(x), then the functions are reflections over Y-axis and if - f(x) = g(x), then the functions are reflections over X-axis.

We have,

`f(-x)=2^(-x)=\left((1)/(2)\right)^x=g(x),\\\\-f(x)=-2^x\\eq g(x).`

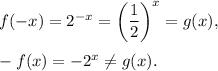
So, the function g(x) is a reflection of f(x) over Y-axis.

The graph of f(x) and g(x) are drawn in the attached file. From there, it is clear that the functions are reflections over Y-axis, not reflections over X-axis.

So, options (A) is incorrect and option (B) is correct.

From the table, we have

`f(-2)=(1)/(4),~~f(-1)=(1)/(2),~~f(0)=1,~~f(1)=2,~~f(2)=4,\\\\g(-2)=4,~~g(-1)=2,~~g(0)=1,~~g(1)=(1)/(2),~~g(2)=(1)/(4).`

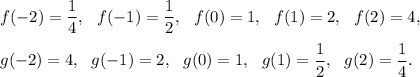
So, as the value of 'x' increases, the value of f(x) increases and value of y(x) decreases.

Therefore, f(x) is an increasing function and g(x) is a decreasing function. So, option (C) is incorrect.

Also, we have

`f(0)=g(0)=1.`

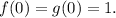
So, both the functions have same initial value. So, option (D) is also incorrect.

Thus, the correct conclusion is (B) The functions f(x) and g(x) are reflections over the y-axis.