Question

Find the horizontal or oblique asymptote of F(x)= -2x^2+3x+6/x+2

Answer 1

f(x)=-2(x^2)+3x+(6/x)+2
fx=2x+3x+(2*3/x)+2
fx={-x*2(x^2)+x(3x)+(2+3)+x*2)/x
result:
fx={-2(x^3)+3(x^2)=2x+6/(x^2)

Answer 2

There is no horizontal asymptote for this function but there is an oblique asymptote which is -2x + 7

Explanation:

When given a function, it is very easy to check its horizontal asymptote,

When dealing with a function say;

`f(x)=(ax^(m) -------)/(ax^(n) -------)`

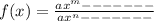
where a and b represents the leading coefficient, m and n represents the degrees, then to find the horizontal asymptote all we need to do is to compare the degree of the polynomials

If m < n then y= 0 That is, if the top degree is less than the bottom degree then the horizontal asymptote is zero(0)

If m = n then y =

That is, if the top degree is equal to the bottom degree, then the horizontal asymptote is equal to where a and b are coefficients of

and

respectively.

If m > n then there is no horizontal asympto

te. That is, if the top degree is greater than the bottom degree, then there is no horizontal asymptote.

Which means there is only a slant asymptote or oblique asymptote

To find the slant asymptote, all we need to do is to use long division to divide our polynomials;

-2x + 7______

x + 2 √-2x² + 3x + 6

-___(-2x - 4x)_____

7x + 6

- (7x +14)

___________________

-8

Therefore the oblique asymptote is -2x + 7