Question

There are given complex numbers

z1=(m-2n-1)+i(5m-4n-6)
z2=(3m-n-6)+i(m-5n-3)
Q: find m and n in a way that z1 and z2 to be conjugated complex numbers, then deternime real and imaginary par of z=z1-z2/conjugated z2

Answer 1

ok... so, we know that both pairs are conjugate of each other,
so.. both are complex solutions, namely, both are a+bi type

what's "a", we dunno, what is "b", we dunno either
but for z1, we know that a = m-2n-1 and b = 5m-4n-6
for z2, a = 3m-n-6 and b=m-5n-3

for those two folks to be conjugate of each other, they'd be
(a+bi)(a-bi)
notice, the "a"s are the same on z1 as well as z2
the "b" are the same also BUT the z2 "b" is negative,
in order to be a conjugate, regardless of that, the "b"s are the same

so, whatever (m-2n-1) is, is the same as (3m-n-6), since a = a
and whatever (5m-4n-6) is, will be the same value, since b =b,
the "a" and "b" in each conjugate, is the same value, thus one can say

`\begin{array}{cccll} z1=&(m-2n-1)+i&(5m-4n-6)\\ &\uparrow &\uparrow \\ &a&b\\ &\downarrow &\downarrow \\ z2=&(3m-n-6)+i&(m-5n-3) \end{array} \\ \quad \\ \begin{cases} m-2n-1=3m-n-6\implies 0=2m+n-5\\ 5m-4n-6=m-5n-3\implies 4m+n-3=0 \end{cases} \\ \quad \\ \textit{now, solving that by using elimination}`


`\begin{array}{llcll} 2m+n-5=0&\leftarrow * -2\implies &-4m-2n+10=0\\ 4m+n-3=0&&4m+n-3=0\\ &&\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\\ &&-n+7=0 \end{array} \\ \quad \\ or\qquad 7=n`

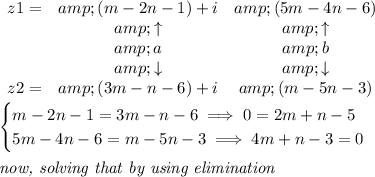
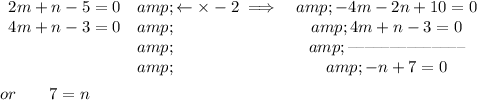
and pretty sure you can find "m" from there
once you have both, substitute in z1 or z2, to get the values for "a" and "b"