Question

A store sells different kinds of candy at $1, $1.50, $2, and $3 per kilogram. How many kilograms of each kind of candy does $3 buy? Explain why the price of 1 kg and the amount of candy that $3 can buy are inversely proportional quantities?

Answer 1

Answer and Explanation:

Given : A store sells different kinds of candy at $1, $1.50, $2, and $3 per kilogram.

To find : How many kilograms of each kind of candy does $3 buy?

Explain why the price of 1 kg and the amount of candy that $3 can buy are inversely proportional quantities?

Solution :

The total amount spent on buying candies is $3.

A store sells different kinds of candy at $1, $1.50, $2, and $3 per kilogram.

When the cost of candies is $1 per kg.

Amount of candies bought is
`(3)/(1)=3\ kg`

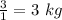
When the cost of candies is $1.50 per kg.

Amount of candies bought is
`(3)/(1.50)=2\ kg`

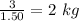
When the cost of candies is $2 per kg.

Amount of candies bought is
`(3)/(2)=1.5\ kg`

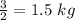
When the cost of candies is $3 per kg.

Amount of candies bought is
`(3)/(3)=1\ kg`

`\text{Unit price of candies}\propto\frac{1}{\text{Amount of candies}}`

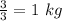
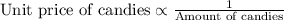
The amount spent on candies is constant.

`\text{Constant of variation}=\frac{\text{Difference in unit price of candies}}{\text{Difference in the amount of candies}}`

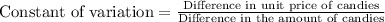
The difference in the unit price of candies = 3-2=1

The difference in the amount of candies = 1-1.5=-0.5

`\text{Constant of variation}=(1)/(-0.5)=-2`

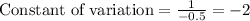
The negative sign indicates the inverse proportionality.