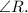Final answer:
Using the Law of Cosines, the length that can be found is
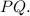
Step-by-step explanation:
The Law of Cosines is expressed as:
![\[ c^2 = a^2 + b^2 - 2ab \cos(C) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/lh1ae0tp11k3pzzyrcr3.png)
where c is the side length across from angle C , and a and b are the other two side lengths of the triangle.
In the given triangle PQR , if angle R measures 18°, and q and p are known, we can use the Law of Cosines to find the length of side PQ , which is opposite to angle R .
Let

![\[ PQ^2 = PR^2 + QR^2 - 2 \cdot PR \cdot QR \cdot \cos(\angle R) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xc9i5tczfwa27h3orec4.png)
Substituting the given values:
![\[ PQ^2 = p^2 + q^2 - 2 \cdot p \cdot q \cdot \cos(18°) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2dqk5fngmb6h6mg3hvjx.png)
Now, calculate the numerical value of PQ using the provided values of p , q , and