Answers:
Part A.
C. AD = AE
Part B.
BC = 26
Step-by-step explanation:
Part A.
If DE is a midsegment of triangle ABC, D is a point that divides AB into two equal segments, so option A. 1/2 AB = AD is true.
Additionally, if DE is a midsegment of triangle ABC, its length is equal to half the length of the side that the segment doesn't cross. So:
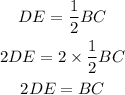
Therefore, option B is also true.
Triangle ABC is scalene, it means that all their sides have different length, it means that AD is not equal to AE and option C is not true.
Finally, segments AE and EC form AB, so:
AC = AE + EC
AC - AE = AE + EC - AE
AC - AE = EC
So, option D is also true.
Therefore, the answer for part A is C. AD = AE
Part B.
We know that 2DE = BC, so replacing the expression for each segment, we get:
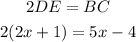
Solving for x:
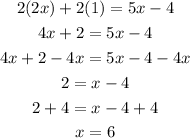
Now, with the value of x, we get that BC is equal to:
BC = 5x - 4
BC = 5(6) - 4
BC = 30 - 4
BC = 26
So, the answer for part B is 26.