Question

Given that DE is the midsegment of the scalene AABC, answer theprompts to the right.

Answer 1

Answers:

Part A.

C. AD = AE

Part B.

BC = 26

Step-by-step explanation:

Part A.

If DE is a midsegment of triangle ABC, D is a point that divides AB into two equal segments, so option A. 1/2 AB = AD is true.

Additionally, if DE is a midsegment of triangle ABC, its length is equal to half the length of the side that the segment doesn't cross. So:

`\begin{gathered} DE=(1)/(2)BC \\ 2DE=2*(1)/(2)BC \\ 2DE=BC \end{gathered}`

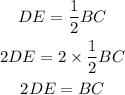
Therefore, option B is also true.

Triangle ABC is scalene, it means that all their sides have different length, it means that AD is not equal to AE and option C is not true.

Finally, segments AE and EC form AB, so:

AC = AE + EC

AC - AE = AE + EC - AE

AC - AE = EC

So, option D is also true.

Therefore, the answer for part A is C. AD = AE

Part B.

We know that 2DE = BC, so replacing the expression for each segment, we get:

`\begin{gathered} 2DE=BC \\ 2(2x+1)=5x-4 \end{gathered}`

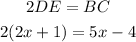
Solving for x:

`\begin{gathered} 2(2x)+2(1)=5x-4 \\ 4x+2=5x-4 \\ 4x+2-4x=5x-4-4x \\ 2=x-4 \\ 2+4=x-4+4 \\ x=6 \end{gathered}`

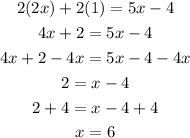
Now, with the value of x, we get that BC is equal to:

BC = 5x - 4

BC = 5(6) - 4

BC = 30 - 4

BC = 26

So, the answer for part B is 26.