The angle between the two ropes, rounded to the nearest degree, is
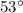 . Therefore, option B is correct
. Therefore, option B is correct
To find the angle between the two vectors
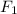 and
and
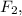 we will:
we will:
1. Calculate the dot product of
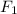 and
and
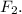
2. Find the magnitudes (or lengths) of
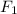 and
and
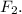
3. Use the dot product and magnitudes to calculate the cosine of the angle between the two vectors.
4. Use the arccosine function to find the angle itself.
5. Convert the angle from radians to degrees.
Given:
![\[ F_1 = (11,000, 5,000) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/ks4f1ozj4djnbzkyfgc1.png)
![\[ F_2 = (14,500, -8,000) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/kp1svts3xy080h7wzmb4.png)
The dot product
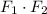 is calculated as:
is calculated as:
![\[ F_1 \cdot F_2 = (11,000 \cdot 14,500) + (5,000 \cdot -8,000) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/9ojkef14i8fm7qng2ygy.png)
The magnitudes of
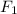 and
and
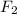 are calculated as:
are calculated as:
![\[ |F_1| = √((11,000)^2 + (5,000)^2) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/5e9ne0mrwgxi7onuwqtd.png)
![\[ |F_2| = √((14,500)^2 + (-8,000)^2) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/oa30h3wqomn0zguqrj4m.png)
The cosine of the angle
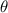 is:
is:
![\[ \cos(\theta) = (F_1 \cdot F_2)/(|F_1| \cdot |F_2|) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/gmn39pj7clgjcem50e8t.png)
Finally, the angle
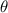 is:
is:
![\[ \theta = \arccos\left((F_1 \cdot F_2)/(|F_1| \cdot |F_2|)\right) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/zzbt6lttap8cymui3edr.png)
Now we will calculate these values step by step:
1. Dot Product: The dot product of the vectors \( F_1 \) and \( F_2 \) is calculated by multiplying corresponding components and then summing those products:
![\[ \text{Dot Product} = F_1 \cdot F_2 = (11,000 \cdot 14,500) + (5,000 \cdot (-8,000)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/3974f64xpob7eex9d3zm.png)
![\[ \text{Dot Product} = 159,500,000 - 40,000,000 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/9yuee4xrsnift4xm9idq.png)
![\[ \text{Dot Product} = 119,500,000 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/htd01ob6jrr4lgf45x3e.png)
2. **Magnitude of \( F_1 \)**: The magnitude (or length) of vector \( F_1 \) is calculated using the Pythagorean theorem for the vector components:
![\[ |F_1| = √(11,000^2 + 5,000^2) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/jfftlcnr6wuor2dn7q6e.png)
![\[ |F_1| = √(121,000,000 + 25,000,000) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/ph9zy5knuuuytlxa2jvo.png)
![\[ |F_1| = √(146,000,000) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/usz6ii9z2ptcm1wbej17.png)
![\[ |F_1| \approx 12,083.05 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/a2vqwzhpd4nsbcckrtqp.png) (rounded to two decimal places for clarity)
(rounded to two decimal places for clarity)
3. Magnitude of
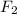 : Similarly, the magnitude of vector
: Similarly, the magnitude of vector
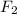 is:
is:
![\[ |F_2| = √(14,500^2 + (-8,000)^2) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/e7s2rorty10eeg2jv8a7.png)
![\[ |F_2| = √(210,250,000 + 64,000,000) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/c0nsnagmy1banqosodkj.png)
![\[ |F_2| = √(274,250,000) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/n71zfkzcj15a7jhtarj9.png)
![\[ |F_2| \approx 16,560.50 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/yt93frxe6sgappu5ynzo.png) (rounded to two decimal places for clarity)
(rounded to two decimal places for clarity)
4. Cosine of the Angle: The cosine of the angle between the vectors is the dot product divided by the product of the magnitudes:
![\[ \cos(\theta) = \frac{\text{Dot Product}} \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/1in0gwpkrs13pftef2b6.png)
![\[ \cos(\theta) = (119,500,000)/(12,083.05 \cdot 16,560.50) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/91t5k9ra4kc0yzjlnwx0.png)
![\[ \cos(\theta) \approx (119,500,000)/(200,139,302.5) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/7ailbxbzn1t0ajxzhjie.png)
![\[ \cos(\theta) \approx 0.5972 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/i6t48gmu9hnyjeaqj0go.png) (rounded to four decimal places for clarity)
(rounded to four decimal places for clarity)
5. Angle
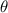 : To find the angle in radians, we use the arccosine function:
: To find the angle in radians, we use the arccosine function:
![\[ \theta = \arccos(\cos(\theta)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/sxeekae1macngt5s0fe2.png)
![\[ \theta \approx \arccos(0.5972) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/s9uzuo7w6ko83zj6uele.png)
![\[ \theta \approx 0.9303 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/hrnbpqwu3o5twueyznt9.png) (in radians, rounded to four decimal places)
(in radians, rounded to four decimal places)
6. Convert to Degrees: Finally, convert the angle from radians to degrees:
![\[ \theta \text{ in degrees} = \frac{\theta \text{ in radians}}{\pi} * 180^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/aebgpqiht60gkcecheqi.png)
![\[ \theta \text{ in degrees} \approx (0.9303)/(\pi) * 180^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/f4cshqnvw9zirliwlpnj.png)
![\[ \theta \text{ in degrees} \approx 53.33^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/qak7vj5qfgm5z45nybub.png)
Rounded to the nearest degree, the angle is
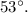
The angle between the two ropes, rounded to the nearest degree, is
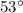 .
.