Question

A set of normally distributed data has a mean of 485 and a standard deviation of 11.6. Find the probability of randomly selecting 40 values and getting a mean less than 490.

Answer 1

Answer:0.9968

Explanation:

prob/stats

Answer 2

Let
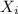
`X_i` denote a data point taken from the distribution, where
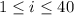
`1\le i\le40`, and let
`Y` denote the average.

You want to find


`\mathbb P\left(\displaystyle\frac1{40}\sum_(i=1)^(40)X_i<490\right)=\mathbb P(Y<490)`

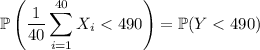
First, let's recall a few things. The PDF of a normal distribution with mean
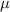
`\mu` and variance
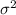
`\sigma^2` is


`f(x;\mu,\sigma^2)=\displaystyle\frac1{\sigma√(2\pi)}\exp\left(-((x-\mu)^2)/(2\sigma^2)\right)`

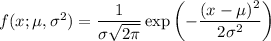
Each of the
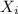
`X_i` are presumably independently selected, so they are i.i.d. random variables.

The MGF of a normal distribution is


`M_X(t)=\mathbb E(e^(tX))`

`M_X(t)=\displaystyle\int_(-\infty)^\infty e^(tx)f_X(x)\,\mathrm dx`

`M_X(t)=\exp\left(\mu t+\frac12\sigma^2t^2\right)`

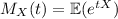
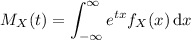
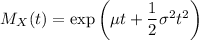
The MGF of a linear combination of i.i.d. random variables is


`M_(c_1X_1+\cdots+c_nX_n)=M_(X_1)(c_1t)*\cdots* M_(X_n)(c_nt)=\displaystyle\prod_(i=1)^nM_(X_i)(c_it)`

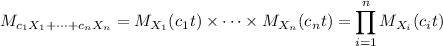
In this case, each
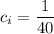
`c_i=\frac1{40}`. This product of MGFs reduces to an MGF of a normal distribution because the
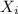
`X_i` are i.i.d..


`M_Y(t)=\displaystyle\prod_(i=1)^(40)M_(X_i)(t)=\exp\left(\mu\left(\frac t{40}\right)+\frac12\sigma^2\left(\frac t{40}\right)^2\right)*\cdots*\exp\left(\mu\left(\frac t{40}\right)+\frac12\sigma^2\left(\frac t{40}\right)^2\right)`

`M_Y(t)=\exp\left(\mu t+\frac12\left(\frac\sigma{√(40)}\right)^2t^2\right)`

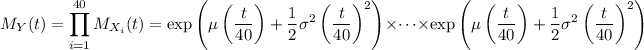
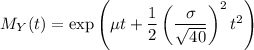
which is indeed the MGF of a normal distribution with mean
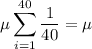
`\displaystyle\mu\sum_(i=1)^(40)\frac1{40}=\mu` and variance
`\sigma^2\displaystyle\sum_(i=1)^(40)\left(\frac1{40}\right)^2=(\sigma^2)/(40)`

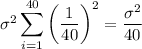
So, the PDF of
`Y`, given that
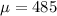
`\mu=485` and
`\sigma=11.6`, is


`f_Y(y)=\displaystyle\frac1{(11.6)/(√(40))√(2\pi)}\exp\left(-((y-485)^2)/(2\left((11.6)/(√(40))\right)^2)\right)`

Now,


`\mathbb P(Y<490)=\displaystyle\int_(-\infty)^(490)f(y)\,\mathrm dy`

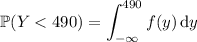
or, using the CDF of
`Y`,


`\mathbb P(Y<490)=F_Y(490)\approx0.9968`