Answer:
The center of the circle is (2, -8)
Explanation:
Given : the equation of circle as
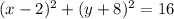
We have to find the center of the circle whose equation is
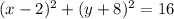
The general equation of a circle is given as
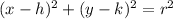
Where , (h,k) represents the center of the circle and r represents the radius of the circle.
Comparing the given equation of circle
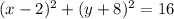 with the general we get,
with the general we get,
h = 2 , k = -8 and r = 4
Thus
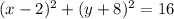 can be written as
can be written as
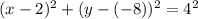
Thus, the center of the circle is (2, -8)