Question

Which of the following integrals represents the area of the region bounded in the first quadrant by x = pi/ 4 and the functions f(x) = sec^2(x) and g(x) = sin(x)?

Answer 1

option B is true.

Explanation:

We are given that two functions

f(x)=
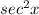`sec^2x` and g(x)=sin x and a line x =
`(\pi)/(4)`

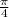
We have to find the area of the region bounded in the first quadrant by x=
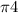`{\pi}{4}` and two functions

We know that the area bounded by two functions

=Integration of region(Upper curve- lower curve)

Therefore, function of sec square x is upper curve and function of sin x is lower function

Therefore, limit of x changing from 0 to
`(\pi)/(4)`

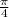
Hence, the area of the region bounded in the first quadrant and two functions is given by

`=\int_(0)^{(\pi)/(4)} (sec^2x-sinx) dx`

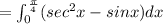
Therefore, option B is true.