Question

CALC HELP!
16
18
8
32

Answer 1

`\displaystyle 2 + \int\limits^6_2 {g(x)} \, dx = 18`

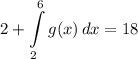
General Formulas and Concepts:

Calculus

Integration

• Integrals

Integration Property [Flipping Integral]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = -\int\limits^a_b {f(x)} \, dx`

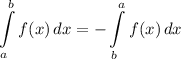
Integration Property [Splitting Integral]:
`\displaystyle \int\limits^c_a {f(x)} \, dx = \int\limits^b_a {f(x)} \, dx + \int\limits^c_b {f(x)} \, dx`

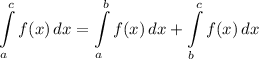
Explanation:

Step 1: Define

Identify

`\displaystyle \int\limits^8_2 {g(x)} \, dx = 13`

`\displaystyle \int\limits^8_6 {g(x)} \, dx = -3`

`\displaystyle 2 + \int\limits^6_2 {g(x)} \, dx`

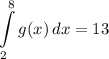
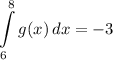
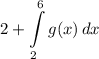
Step 2: Integrate

1. [Integral] Rewrite [Integration Property - Flipping Integral]:
   `\displaystyle \int\limits^8_6 {g(x)} \, dx = -3 \rightarrow \int\limits^6_8 {g(x)} \, dx = 3`
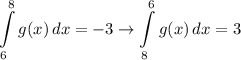
2. [Integral] Rewrite [Integration Property - Splitting Integral]:
   `\displaystyle 2 + \int\limits^6_2 {g(x)} \, dx = 2 + \int\limits^8_2 {g(x)} \, dx + \int\limits^6_8 {g(x)} \, dx`
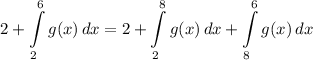
3. [Integrals] Substitute:
   `\displaystyle 2 + \int\limits^6_2 {g(x)} \, dx = 2 + 13 + 3`
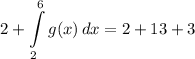
4. Simplify:
   `\displaystyle 2 + \int\limits^6_2 {g(x)} \, dx = 18`

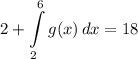
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration