For the coefficients to be rational, any complex roots must occur in conjugate pairs. So if
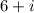
is a root, then so must be
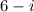
.
Now such a third degree polynomial might be

The only variation to this would be multiplying throughout by some non-zero constant. This doesn't change the roots.