Question

mputing and Using a Least-Squares Regression LineVehiclesight (tons) Gas mileage (mpg)1.6291.6451.75261.952221821211822.32.5The table shows the weight and gas mileage of severalvehicles.What is the equation of the least-squares regressionline, where ŷ is the predicted gas mileage and x is theweight?ŷ=V+According to the regression equation, a car that weighs1.8 tons would have a gas mileage of aboutmiles per gallon.

Answer 1

here's your answer :)

Explanation:

Answer 2

From the table, we have the following points:

(x, y) ==> (1.6, 29), (1.6, 45), (1.75, 26), (1.95, 22), (2, 18), (2, 21), (2.3, 21), (2.5, 18)

Let's find the regression line.

Apply the slope-intercept form:

y = mx + b

Where m is the slope and b is the y-intercept.

To find the slope, apply the formula:

`m=(n(\Sigma xy)-\Sigma x\Sigma y)/(n(\Sigma x^2)-(\Sigma x)^2)`

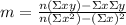
Where:

• ∑x = 1.6 + 1.6 + 1.75 + 1.95 + 2 + 2 + 2.3 + 2.5 = 15.7

• ∑y = 29 + 45 + 26 + 22 + 18 + 21 + 21 + 18 = 200

• ∑xy = 1.6⋅29 + 1.6⋅45 + 1.75⋅26 + 1.95⋅22 + 2⋅18 +2⋅21 +2.3⋅21 + 2.5⋅18 = 378.1

• ∑x² = 1.6² + 1.6² + 1.75² + 1.95² + 2² + 2² + 2.3² + 2.5² = 31.525

,

• n is the number of data = 8

Now, plug in values into the equation and solve for m:

`\begin{gathered} m=(8(378.1)-15.7*200)/(8(31.525)-(15.7)^2) \\ \\ m=-20.175\approx20.2 \end{gathered}`

The slope, m = -20.2

To find the y-intercept, b, apply the formula:

`\begin{gathered} b=((\Sigma y)(\Sigma x^2)-\Sigma x\Sigma xy)/(n(\Sigma x^2)-(\Sigma x)^2) \\ \\ b=(200(31.525)-15.7*200)/(8(31.525)-15.7^2) \\ \\ b=64.594\approx64.6 \end{gathered}`

Therefore, the regression equation is:

y = 64.6 + (-20.2)x

(b). Substitute 1.8 for x in the equation and solve for y:

y = -20.2(1.8) + 64.6

y = 28.24 = 28.

ANSWER:

(A). y = 64.6 + (-20.2)x

(B). 28