Variation of parameters only applies to solving for particular solutions, which require that the ODE is nonhomogeneous. This isn't the case for your equation.
Anyway, the standard approach is to substitute
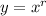
.
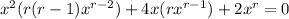

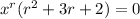
which admits two solutions for

:
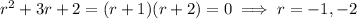
So the complementary solution is
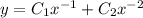
Unless you have a variant of this ODE that is nonhomogeneous, you are done.