What is the difference between bernoulii equation and riccati equation How can i decide any of them in solving 1st order non-linear ODE ??? - QAmmunity.org

What is the difference between bernoulii equation and riccati equation How can i decide any of them in solving 1st order non-linear ODE ???

asked Nov 16, 2018 195k views

1 Answer

The Bernoulli equation is almost identical to the standard linear ODE.

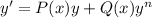
y'=P(x)y+Q(x)y^n

y'=P(x)y+Q(x)y^n

Compare to the basic linear ODE,

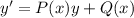
y'=P(x)y+Q(x)

y'=P(x)y+Q(x)

Meanwhile, the Riccati equation takes the form

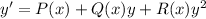
y'=P(x)+Q(x)y+R(x)y^2

y'=P(x)+Q(x)y+R(x)y^2

which in special cases is of Bernoulli type if
P(x)=0

P(x)=0

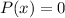
, and linear if
R(x)=0

R(x)=0

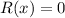
. But in general each type takes a different method to solve. From now on, I'll abbreviate the coefficient functions as
P,Q,R

P,Q,R

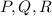
for brevity.

For Bernoulli equations, the standard approach is to write

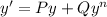
y'=Py+Qy^n

y'=Py+Qy^n

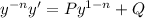
y^(-n)y'=Py^(1-n)+Q

and substitute
v=y^(1-n)

v=y^(1-n)

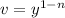
. This makes
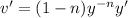
v'=(1-n)y^(-n)y'

v'=(1-n)y^(-n)y'

, so the ODE is rewritten as

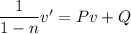
$\frac1{1-n}v'=Pv+Q$

and the equation is now linear in

.

The Riccati equation, on the other hand, requires a different substitution. Set
v=Ry

v=Ry

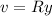
, so that
$v'=R'y+Ry'=R'\frac vR+Ry'$ . Then you have

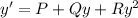
y'=P+Qy+Ry^2

y'=P+Qy+Ry^2

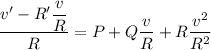
$\frac{v'-R'\frac vR}R=P+Q\frac vR+R(v^2)/(R^2)$

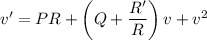
$v'=PR+\left(Q+\frac{R'}R\right)v+v^2$

Next, setting
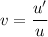
$v=\frac{u'}u$ , so that
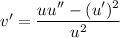
v'=(uu''-(u')^2)/(u^2)

v'=(uu''-(u')^2)/(u^2)

, allows you to write this as a linear second-order equation. You have

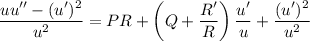
$(uu''-(u')^2)/(u^2)=PR+\left(Q+\frac{R'}R\right)\frac{u'}u+((u')^2)/(u^2)$

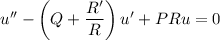
$u''-\left(Q+\frac{R'}R\right)u'+PRu=0$

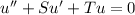
u''+Su'+Tu=0

u''+Su'+Tu=0

where
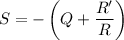
$S=-\left(Q+\frac{R'}R\right)$ and
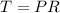
T=PR

T=PR

.

Mgilbert answered Nov 20, 2018

9.1k points

Search QAmmunity.org