Question

In a given isosceles triangle, the vertex angle measures 150°. If the base of the triangle is 17 cm, then

what is the perimeter of the isosceles triangle?
PLEASE HELP

Answer 1

34.599695067 cm

Explanation:

When you draw the altitude, you have 2 right triangles with angle measures 15, 75, 90

Since it is a right triangle, you can use trignometry to ifind the missing side

If you take the triangle on the right, you have to find the measure of the hypotenuse

Use sine:

sin75 = opposite/hypotenuse

sin75 = 8.5/x

xsin75=8.5

x=8.5/sin75

x=8.79984753349

Perimeter = 2x+17

Answer 2

34.6 cm (nearest tenth)

Explanation:

The altitude of an isosceles triangle is the perpendicular line segment drawn from the vertex (the angle opposite the base) to the base.

Since an isosceles triangle has two congruent legs and two congruent base angles, the altitude bisects the vertex angle and the base, creating two congruent right triangles. (See attachment).

To calculate the perimeter of the triangle, we need to find the length of the legs.

The legs are the hypotenuse of each right triangle.

To find their measures, use the sine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

As the altitude bisects the vertex angle, and the given vertex angle is 150°, the angle is:

• θ = 150°/2 = 75°

As the altitude bisects the base, the side opposite the angle is half of the base of the triangle:

• O = 17/2 = 8.5 cm

Substitute these values into the sine ratio to calculate the length of each leg of each right triangle (H):

`\sin(75^(\circ))=(8.5)/(H)`

`H=(8.5)/(\sin(75^(\circ)))`

`H=8.79984753...`

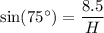
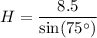
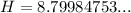
The perimeter of a two-dimensional shape is the distance all the way around the outside. Therefore, the perimeter of the isosceles triangle is the sum of the lengths of its legs and its base:

`\begin{aligned}\sf Perimeter&=\sf Leg+Leg+Base\\&=8.79984753...+8.79984753...+17\\&=34.5996950...\\&=34.6\; \sf cm\;(nearest\;tenth)\end{aligned}`

Therefore, the perimeter of the isosceles triangle is approximately 34.6 cm (rounded to the nearest tenth).