Answer:
Number of bats should be produced to keep costs at a minimum is 60.
Explanation:
Given : The cost, C, to produce b baseball bats per day is modeled by the function
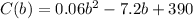 .
.
To find : What number of bats should be produced to keep costs at a minimum?
Solution :
Function in quadratic form is
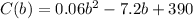
To determine the minimum point we apply the formula of quadratic equation
 is
is
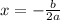
On comparing with given model, a=0.06 , b=-7.2 , c=390
The minimum point is at
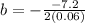
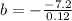
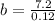
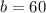
i.e. The minimum number of bats per day is 60.
The cost at b=60 is
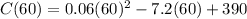
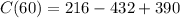
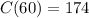
The minimum cost is $174 and minimum number of bats is 60.
We can also determine through graph.
Refer the attached figure below.