Answer:

Explanation:
The polynomial which have four roots that means zero roots of this polynomial will be (x -2), (x -2), (x -3) and (x -3)
So the polynomial will be (x + 2)(x + 2)(x - 3)(x - 3)
= (x + 2)²(x - 3)²
= (x² + 4x + 4)(x² + 9 - 6x)
=
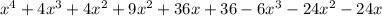
=

Therefore, the polynomial will be (
 )
)